Recursion
| In this article |
|---|
| 1- What is a Recursive function and the problem it solve? |
| 2- Example Computing Powers . |
Recursive function
A Recursive function is a function that calls itself ether directly or indirectly through another function .A Recursive function is called to solve a problem by solving a smaller instance of the same problem unless it is the simplest case(s) or so-called base case(s) it will return the result.
Example Computing Powers
function CopmutePower(x , n){
if (n == 0){
return 1;
}
}
}
2 - The second case we can think about is when n is positive
when you multiply powers of x you add the exponents: x^a * x^b = x^(a+b)
eg. 2^2 × 2^4 = 2^(2+4) = 64.
If n is positive and even then x^n = x^(n/2) * x^(n/2)
eg. 2^6 = 2^(6/2) * 2^(6/2) = 64 and for y= x^(n/2) Therefore x^n = y * y
function CopmutePower(x , n){
// n = 0 Simplest case(base case)
if (n == 0){
return 1;
}
// n is positive even
}
// n is positive even
if (n % 2 == 0){
var y = CopmutePower(x, n / 2);
return y * y;
}
}
3 -If n is positive and odd then x^n = x^(n−1) * x in this case if n-1 = 0 then it will be the base case when n = 0 and if n-1 is positive and even then it will be the second case .
Therefor you could compute those cases recursively
function CopmutePower(x , n){
// n = 0 Simplest case(base case)
if (n == 0){
return 1;
}
// n is positive and even
}
// n is positive and even
if (n % 2 == 0){
var y = CopmutePower(x, n / 2);
return y * y;
}
// n is positive and even
if (!(n % 2 == 0)){// n is positive and even
return x * CopmutePower(x, n - 1);
}
}
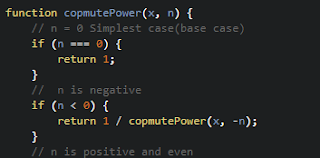
4 - If n is negative then x^n = 1 / (x^n)
function CopmutePower(x , n){
// n = 0 Simplest case(base case)
if (n == 0){
return 1;
}
// n is positive and even
}
// n is positive and even
if (n % 2 == 0){
var y = CopmutePower(x, n / 2);
return y * y;
}
// n is positive and even
if (!(n % 2 == 0)){// n is positive and even
return x * CopmutePower(x, n - 1);
}
if (n < 0){
return 1 / CopmutePower(x, -n);
}
}
-- JavaScript Code
-- C# Code